Describe the Continuity or Discontinuity of the Graphed Function
We can see that left limit is not equal to right limit. The function graphed below is NOT continuous everywhere it is discontinuous at x 2 and.

Lots Of Points Urgent Describe The Continuity Or Discontinuity Of The Graphed Function Brainly Com
Since square root is there we find that x can only be posiitve but y can be since square root both positive and negative.
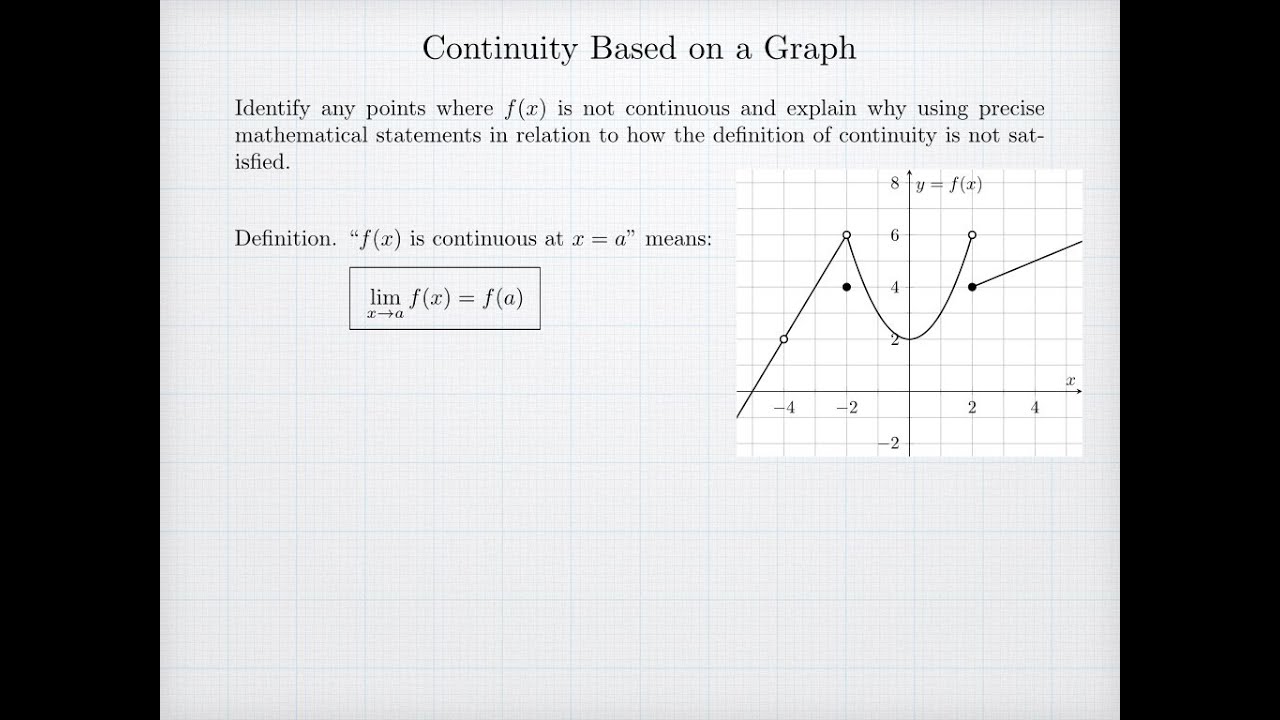
. X 1 x6 D. The graph below shows a function that is discontinuous at xa. A function is continuous if we can ensure arbitrarily small changes by restricting enough minor changes in its input.
Take a screen shot of each save in a word document. When this happens we say the function has a jump discontinuity at xa. So limit does not exist.
Since limit does not exists. Discuss the continuity of the function fx sin x. Describe the continuity of the graphed function.
The function has an infinite discontinuity at x 3. X -1 x 6 C. The lim fx as x approaches c exists 3.
Without a graph to look at how can we determine if a function is continuous or not. If the given function is not continuous then it is said to be discontinuous. So this function is discontinuous at x3.
The function has a nonremovable. When graphed a removable discontinuity or a hole is just a missing value in the function. We can see that this curve is smooth everywhere except at x-1.
Fc is defined 2. Go through the continuity and discontinuity examples given below. So we will check continuity at x-1.
So this function is discontinuous at x-1. Calculus gives us a way to test for continuity using limits instead. Any function fx is continuous at xa only if.
1 point O The function has a removable discontinuity at x 3. A function is continuous when its graph is a single unbroken curve that you could draw without lifting your pen from the paper. A continuous function can be graphed as a single connected curve.
Discontinuity may be removable point infinite and jump with functions that fail at least one of the three conditions. The lim fx as x approaches c fc. Continuous Function At the basic level teachers tend to describe continuous functions as those whose graphs.
When is a function discontinuous. Find any points for the discontinuity for the rational function. Calculus proves that a function is continuous when x a only under three conditions.
The function has a jump discontinuity at x 3. Graphing functions can be tedious and for some functions impossible. X1 x -6 Calculus - Discontinuity.
The function is continuous. I ii 3Tan2x1 iii 2 X1 Cos 3x each 2marks b Determine the discontinuities of the following functions and state why the function fails to be continuous at those points. Precalculus questions and answers.
The function has a removable discontinuity at x 3. In this chapter well use graphs and formulas to describe continuity. Describe the continuity of the graphed function.
So we will check continuity at x3. Continuity A function is a continuous at a point if its graph has no gaps holes breaks or jumps at that point. We have to graph this function and check which list of points lie on the graph.
The function has a nonremovable discontinuity at x 3. Everything else looks like a continuous graph. I think the answer is D.
The function graphed below is continuous everywhere. Use the graph to answer the question also the one I put in the attachment. We can also talk about the continuity or discontinuity of functions.
A continuous function then moves toward each value in a predictable way and actually takes on that value. The correct answer is B because it is increasing at points -10 and 10 or 1infinity. We can see that left limit is not equal to right limit.
More formally a function fx is continuous at a point c if. у 10 сл х 10 -10 -5 5 -5 -10 Use the graph to answer the question. We can see that this curve is smooth everywhere except at x3.
If we define that missing point we will have removed. The arrows on the function indicate it will grow infinitely large as x approaches a. So limit does not not exist.
If a function is not continuous at a point then we say it is discontinuous at that point. If a function contains breaks that function isnt continuous. In mathematics a continuous function is a function that does not have discontinuities that means any unexpected changes in value.
The function is approaching different values depending on the direction x is coming from. Since limit does not exist. Describe the continuity or discontinuity of the graphed function.
Continuity and Discontinuity Examples. Learn about continuity in calculus and see examples of testing for continuity in both graphs and equations. The function has a removable discontinuity at x 0.
Any function fx is continuous at xa only if. If a function contains breaks that function isnt continuous. We know that sin x and cos x are the continuous function the product of sin x and cos x should also be a continuous function.
I was looking for the whole function however it only asked for which interval is the function increasing on. Create graphs of three functions below to determine if they are continuous or discontinuous. There are no sudden jumps and no missing values.
When the function value and limit value are equal at the same point the function is described as continuous at that point. If there is any break in the graph the function has a point of discontinuity. The The function is continuous.

Describe The Continuity Or Discontinuity Of The Graphed Function I Will Give More Points And Brainly Com
7 Continuous And Discontinuous Functions
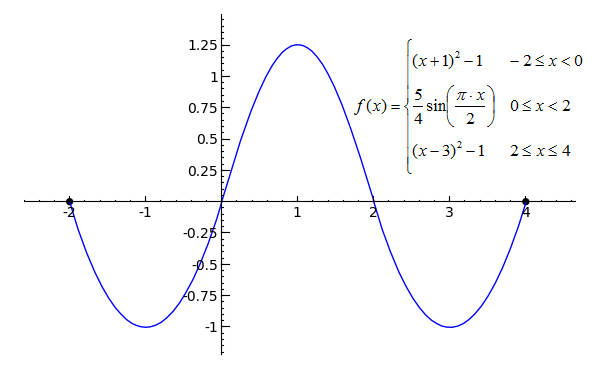
Sage Calculus Tutorial Continuity
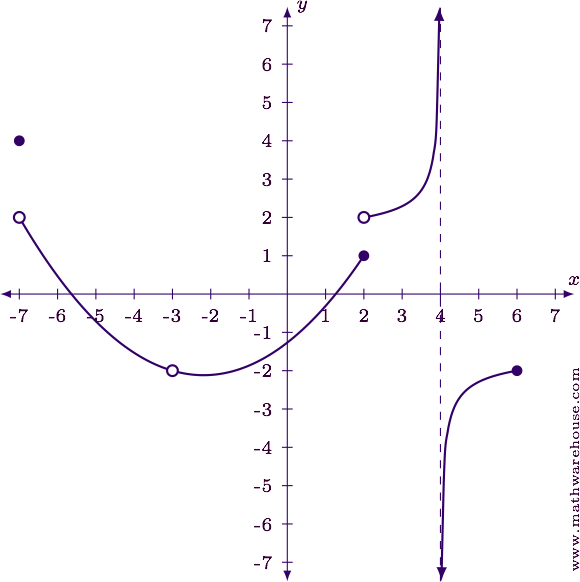
How To Classify Discontinuities

2 4 Continuity Calculus Volume 1
Use The Graph To Answer The Question 4 Describe Gauthmath
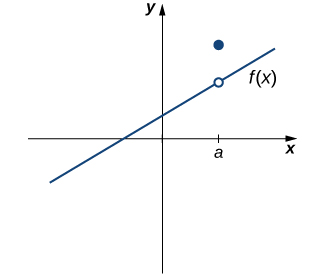
2 4 Continuity Calculus Volume 1

Form A Graphing Continuity And Limits With Rational Functions Rational Function Ap Calculus Ap Calculus Ab

Continuity Of A Function Using A Graph Youtube
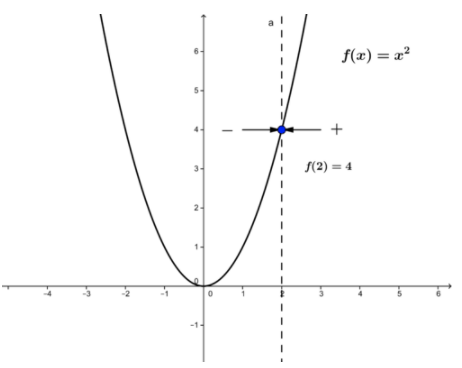
3 1 Continuity Of A Function K12 Libretexts
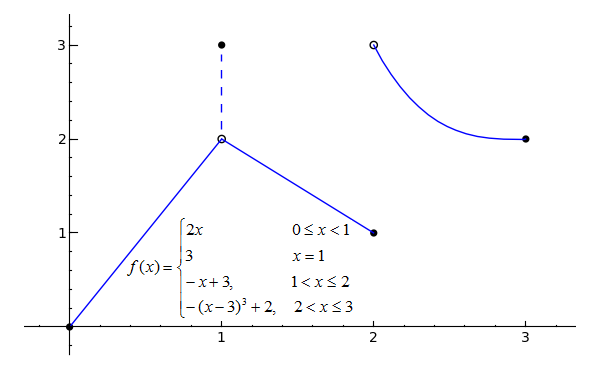
Sage Calculus Tutorial Continuity
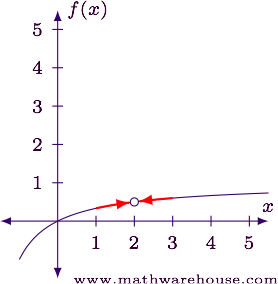
What Are The Types Of Discontinuities Explained With Graphs Examples And Interactive Tutorial



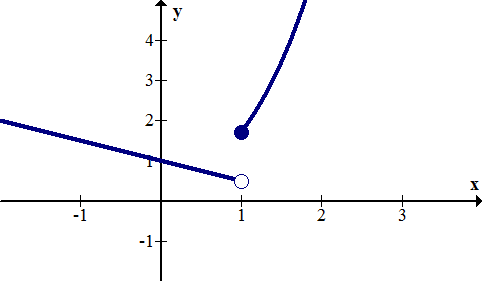


Comments
Post a Comment